Who am I
Greetings!! I'm a research scientist at CEA—French Atomic Energy and Alternative Energies Commission. My expertise includes high performance computing, finite element method, Boltzmann transport, and meshing. I hold a PhD in computational physics, a master's in computational fluid dynamics, and a bachelor's in aerospace engineering. In a nutshell, I'm the wizard of numbers and equations, blending science and technology to unlock the secrets of the universe.
Areas of Research
- Finite Element Methods
- Parallel computing
- Meshing
- Mesh Adaption
- Radiative transport
- Computational Fluid Dynamics
Codes that I am developing
SALOMEPre/post-processing scientific computing tool for CAD, meshing, visualization
ArcaneFEMParallel FEM solver based on CPU-GPU parallelism
PSDMassively parallel Solid/Structural/Seismic Dynamics FEM solver
top-ii-volMassively parallel geophysics mesher-partitioner tool
PDMTParallel Dual Meshing Tool, is a polyhedral meshing/remsehing too
mediolibrary that facilitates input and output of mesh files for FreeFEM in the med format
Current areas of research
Polyhedral Meshing
Polyhedral meshing is gaining importance in modern computational simulations. It offers advantages in terms of accuracy, adaptability to complex geometries, efficiency in parallel computing, and improved convergence of numerical solvers. These benefits make polyhedral meshing a valuable tool in various scientific and engineering applications.
Load more
Mesh Adaption
Mesh adaptation is crucial in computational simulations as it enables the dynamic adjustment of the mesh based on evolving solution characteristics. By refining or coarsening the mesh in specific regions, mesh adaptation improves accuracy in critical areas, reducing computational costs by avoiding unnecessary refinement elsewhere. This is particularly important for capturing complex geometries, handling singularities, and optimizing element types, ensuring efficient and reliable simulations. Mesh adaptation in a nutshell helps in making simulations more robust in dynamic environments.
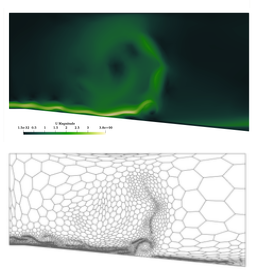
Load more
Finite Element Solver (CPU/GPU)
A parallel FEM solver is indispensable in many computational simulations as it leverages the power of parallel processing to tackle complex and large problems more efficiently. By dividing the computational workload among multiple processors (CPU/GPU/Threads), parallel FEM solvers dramatically reduce simulation time for large-scale models. This is particularly crucial in fields such as structural mechanics, fluid dynamics, and electromagnetics, where simulations involve intricate geometries and intricate physical interactions.
Load more
HPC for Fracture
HPC plays a vital role in advancing phase-field fracture FEM simulations. The intricate nature of fracture phenomena demands substantial computational resources for phase-field simulations due to fine meshing constrain. HPC enables the efficient handling of fine mesh refinements necessary for accurately tracking crack initiation and propagation. Not only this, HPC is also indispensable for enhancing the accuracy, efficiency, and scalability of phase-field fracture simulations, facilitating a deeper understanding of complex fracture mechanics in diverse materials.
FEM-Compliant parallel meshing-partitioning in Geophysics
Past areas of research
Radiative transport in porous media
Load more
